MCMC, Spot Volatility, and Strategic Value of Information

Spot Volatility

This is the major motivation for applying MCMC to smooth the noise part associated with the nonparametric estimation of spot volatility by fixing the local estimation window size. Traditionally, to obtain a relatively satisfactory estimation of spot volatility using nonparametric econometric tools, we need the asymptotic scheme, which is to some extent not that easy to be satisfied in practice for high-frequency trading since a lot of technical issues would be involved when we want to collect and sample data at high-frequency but maintain the number of observations reasonably large enough. This is the major motivation for applying MCMC to smooth noise part associated with the nonparametric estimation of spot volatility by fixing the local estimation window size (Bollerslev, Li and Liao ,2021).

Volatility and Strategic Value of Information

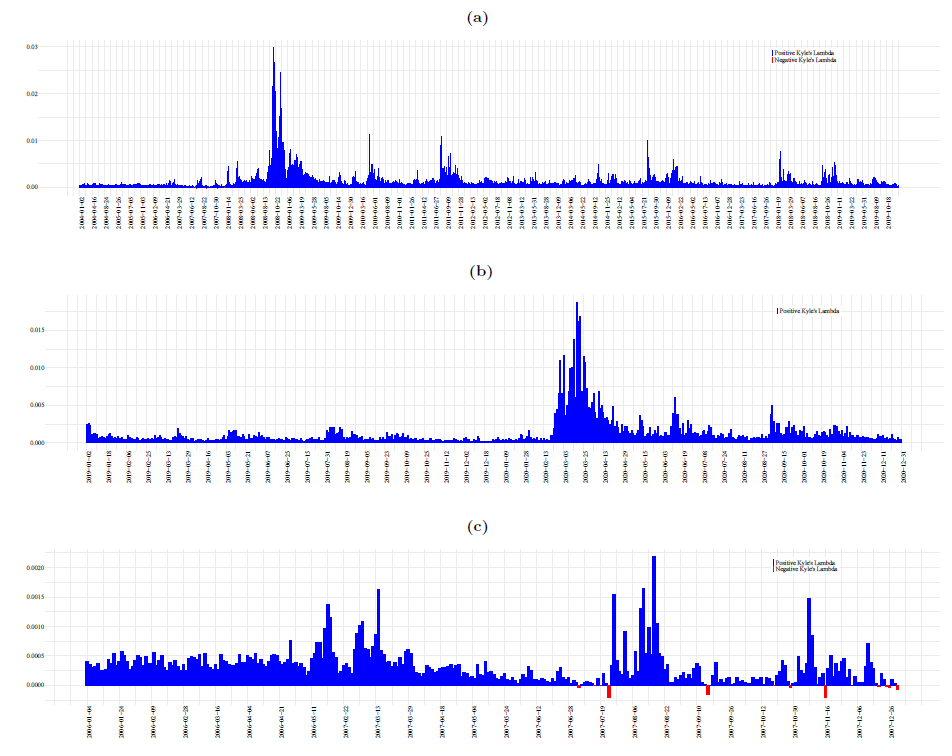
Kyle’s lambda as the measure bridging volatility and value of private information was intially proposed in Kyle (1985), later extended to continuous-timing setting in Back (1992) and more recently discussed in Back (2017). For more technical details and comprehensive discussions, please refer to the literature listed.

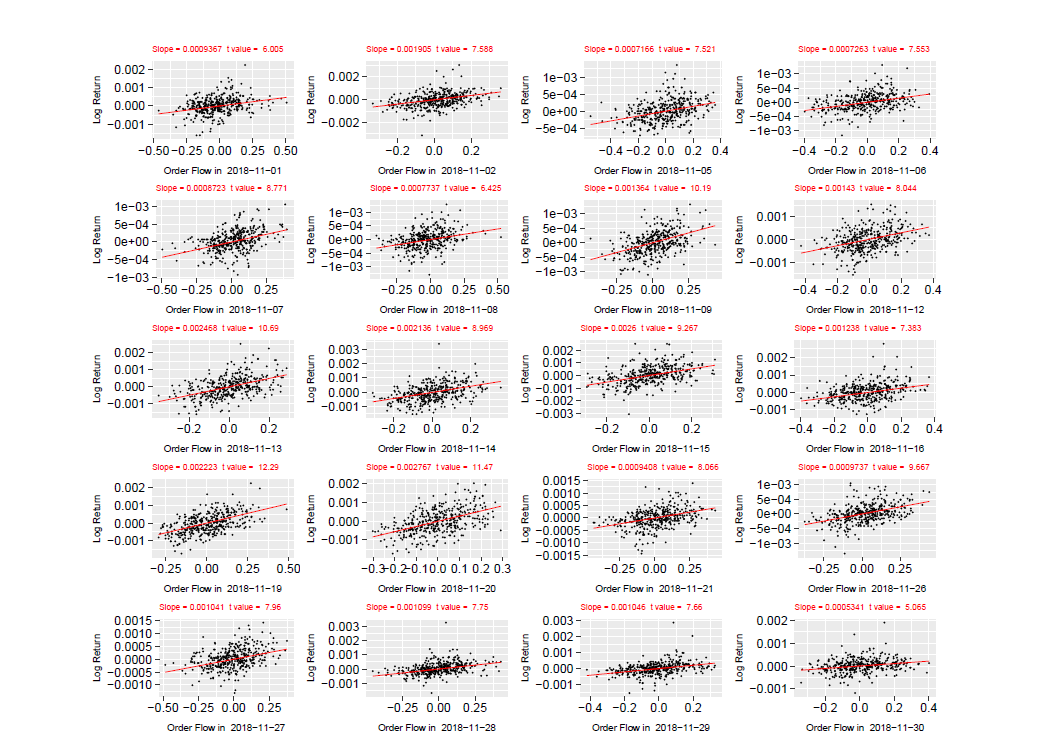
Idea is simple: Regression+Bayesian !!!

For Kyle’s lambda, using following regression to back out the slope as the target Kyle’s lambda. $$ r_{t i}=\lambda_{t} y_{ti}+\varepsilon_{ti} $$ where $r_{ti}$ refers to log return of asset over timing interval $i$ at date $t$: $$ r_{t i}=p_{t \tau_{i}}-p_{t \tau_{i-1}}=\ln P_{t \tau_{i}}-\ln P_{t \tau_{i-1}}. $$ and $y_{ti}=Y_{t\tau_{i}}-Y_{t\tau_{i-1}}$ refers to order flow over interval $i$ at $t$. Besides, it can be demonstrated that strategic value of information can be characterized as $$ \Omega=\mathbb{E}[J(0, \bar{v}, \tilde{v})]=\frac{\sigma_{v}^{2}}{\lambda} P_{0} $$ with $J(t,p,v)$ as the characterizing HJB equation specifying the scheme maximizing accumulated wealth dynamically: $$ J(t, p, v)=\frac{p-v+v(\ln v-\ln p)}{\lambda}+\frac{1}{2} \sigma_{v} \sigma_{z}(1-t) v. $$ Consequently, it is possible for us to estimate strategic value of information as following $$ \hat{\Omega}_{t}=\frac{\hat{\sigma}_{t}^{2}}{\hat{\lambda}_{t}} P_{t-1} $$ by replacing $\hat{\lambda}_{t}$ with slope associated with univariate regression above (Regression) and smoothed Volatility using MCMC (Bayesian).

Is Simple Regression Valid ? Almost Surely !!!